概率分布函数

Discrete Random Variable

离散型随机变量，随机变量的取值是有穷可列举的
通常用大写字母表示随机变量，用小写字母表示随机变量的观测值

Probabolity Mass Function

直译为概率质量函数，教科书常用概率分布，表明随机变量有哪几种取值可能，每种所对应的概率是多少，所以严格来讲应该叫离散型随机变量值分布与概率分布

用数学语言来讲，概率分布是表示所有$P(X=x)$或$p(x)$的图、表、公式

例如抛骰子

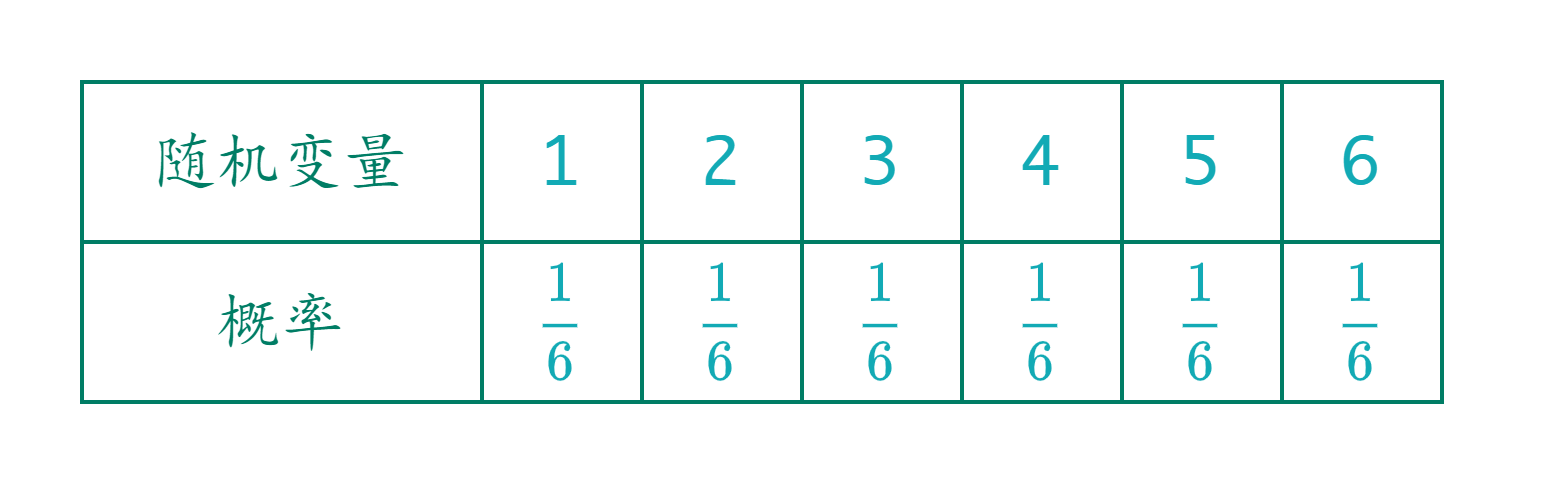
概率分布

Cumulative Distribution Function

直译为累计分布函数，教科书直接叫分布函数，是对概率分布的累加

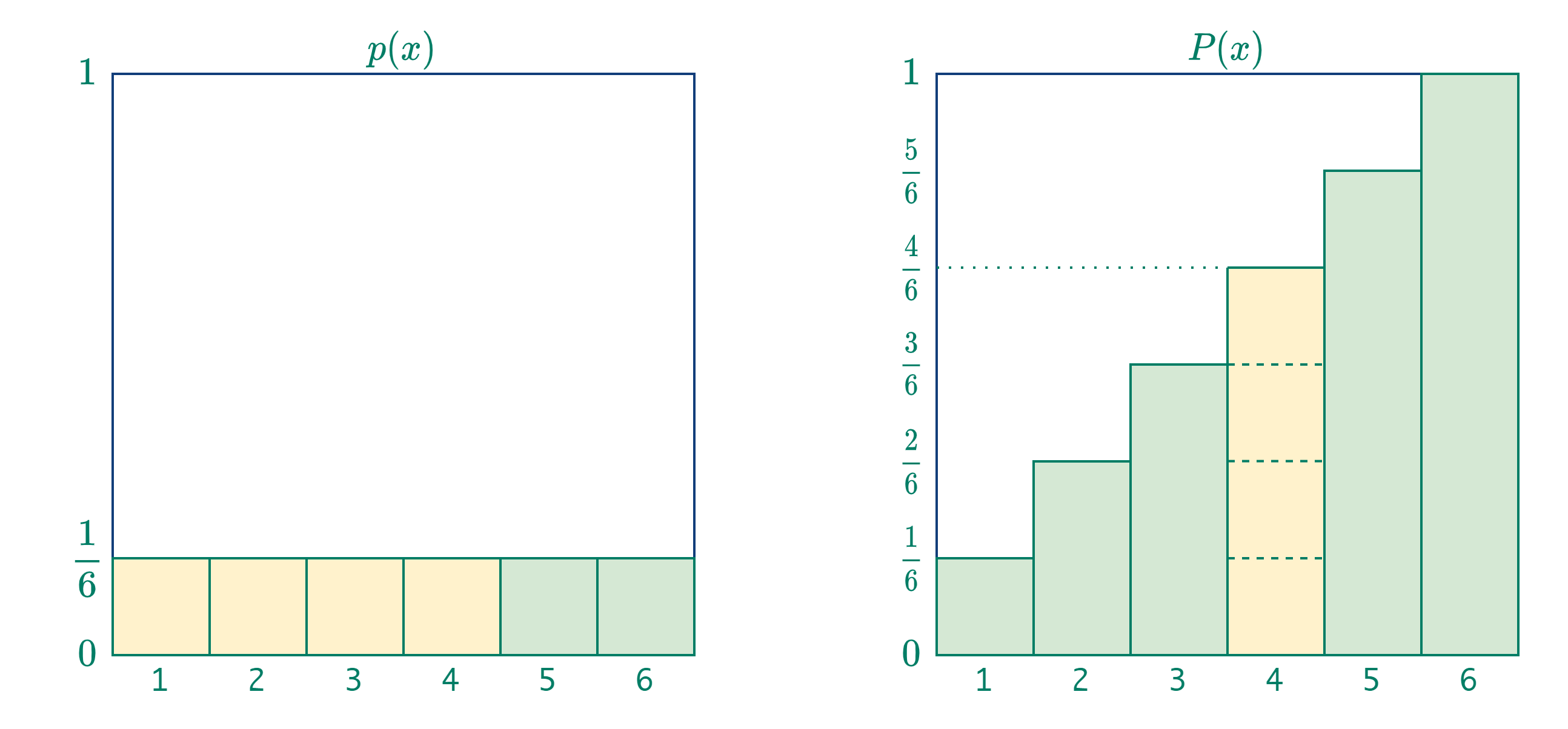
可以看到

$$F_X(x = 4) = \mathbb{P}(X \leq 4) = \sum_{x_i=1}^{4}p(x_i)$$

Expectation/Mean

对于离散随机变量$X$，函数$h(X)$关于变量$X$的期望是

$$\mathbb{E}_{X\sim p(\cdot)}[h(X)] = \sum_{x \in \mathcal{X}}p(x) \cdot h(x)$$

Continuous Random Variable

连续型随机变量

Probability Density Function

连续型随机变量的概率分布，称为概率密度函数

性质：

1. 函数值大于等于0
2. 在区间$(-\infty, +\infty)$上的积分为1
3. 连续型随机变量的取值为区间$(a, b]$，其概率等于概率密度函数在相应区间上的面积

$$\mathbb{P}\left\{a < X \leq b\right\} = F_X(b) - F_X(a) = \int_{a}^{b}f(x)dx$$

Cumulative Distribution Function

连续型随机变量也是叫分布函数，由概率密度函数积分得到

$$\mathbb{P} \left\{X \leq x\right\} = F_X(x) = \int_{-\infty}^{x}f(u)du$$

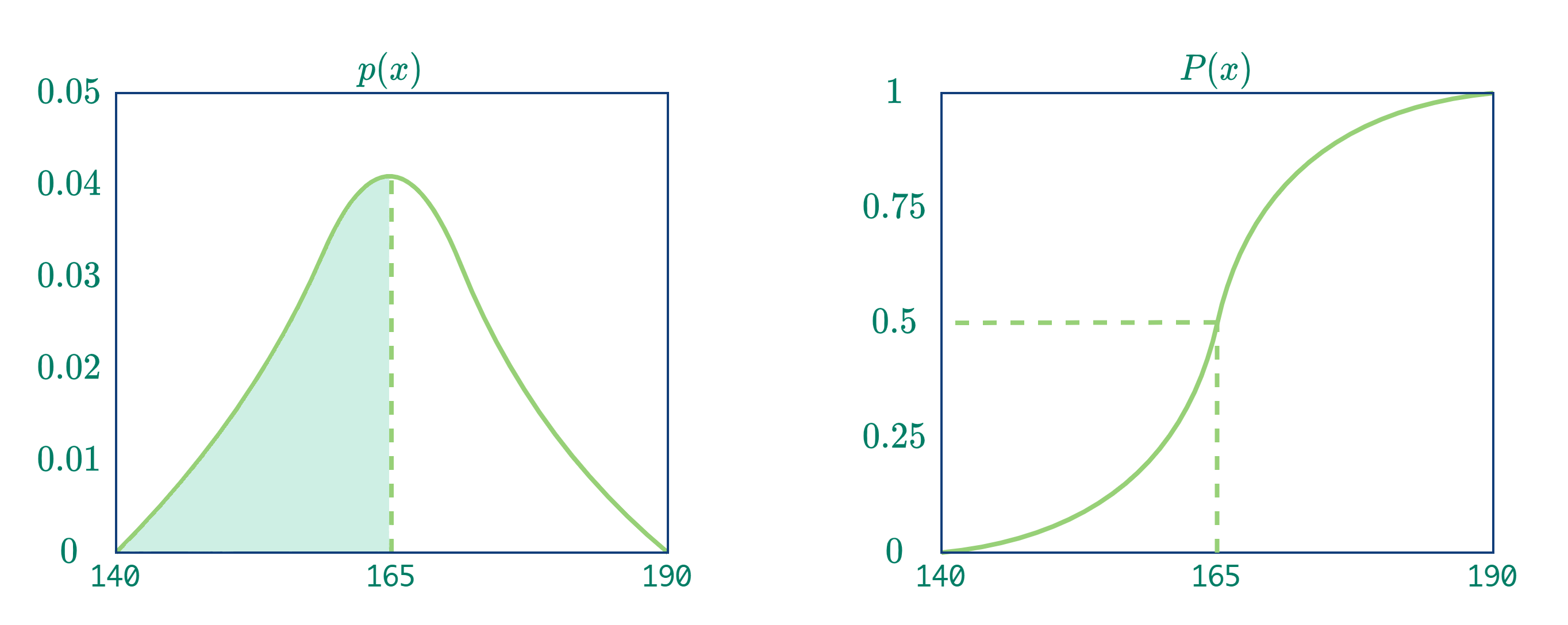
所以，概率密度函数与横轴的面积就是对应分布函数的函数值

Expectation/Mean

对于连续随机变量$X$，概率密度函数为$p(x)$，对$X$求期望

$$\mathbb{E}_{X \sim p(\cdot)}[X] = \int_{\mathcal{X}} x \cdot p(x) dx$$

花体$\mathcal{X}$是随机变量$X$的取值范围

函数$h(X)$关于变量$X$的期望是

$$\mathbb{E}_{X\sim p(\cdot)}[h(X)] = \int_{\mathcal{X}} h(x) \cdot p(x) dx$$

对某个随机随机变量求期望就可以消掉该变量

例如：$g(X,Y)=\frac{1}{5}XY$为二元函数，$X$的取值范围为$[0,10]$，概率密度函数为$p(x)=\frac{1}{10}$，对$X$求期望

$$\begin{align*} \mathbb{E}_{X \sim p(\cdot) }[g(X,Y)] &= \int_{\mathcal{X}}g(x, Y) \cdot p(x) dx \\ &= \int_{0}^{10}\frac{1}{5}xY \cdot \frac{1}{10} dx \\ &= Y \end{align*}$$

可以看到，结果是不含随机变量$X$的，只包含随机变量$Y$

Conditional Expectation/Mean

如果在$Y=y$条件下$X$的条件概率密度函数为$f(x|Y=y)$，那么$X$的条件期望为

$$\mathbb{E}_{X \sim f(\cdot | Y=y)} [X|Y=y] = \int_{\mathcal{X}} x \cdot f(x | Y=y) dx$$

或者直接写成

$$\mathbb{E}_{X \sim f(\cdot | y)} [X|Y=y] = \int_{\mathcal{X}} x \cdot f(x | y) dx$$

从这里可以看出来，对$X$求期望会消掉$X$，所以条件期望$\mathbb{E}[X|Y=y]$的结果是一个$Y=y$条件下的确定的值
如果$Y$没有取值，那$\mathbb{E}[X|Y]$依然是一个关于$Y$的随机变量，有概率密度为$f(y)$，就可以求期望

$$\begin{align*} \mathbb{E}_{Y \sim p(\cdot)} [\mathbb{E} [X|Y] ] &= \int_{\mathcal{Y}} {\color{teal}{\int_{\mathcal{X}} x f(x|y) dx}} \cdot f(y) dy \\ &= \int_{\mathcal{Y}} \int_{\mathcal{X}} x \cdot {\color{Tomato}{f(x|y)f(y)}} dx dy \\ &= \int_{\mathcal{Y}} \int_{\mathcal{X}} x {\color{Tomato}{f(x,y)}} dy \\ &= \mathbb{E}\left[X\right] \end{align*}$$

这里用到了贝叶斯公式

$$f(x|y) = \frac{f(x, y)}{f(y)}$$