定义
半正定矩阵的定义为:给定一个大小为$n \times n$的实对称矩阵$M$,若对于任意长度为$n$的非零向量$X$,有$X^{T}MX \ge 0$恒成立,则矩阵$M$是一个半正定矩阵,若有$X^{T}MX > 0$恒成立,则矩阵$M$是一个正定矩阵
理解:
$X$是向量,$M$看成变换矩阵
向量左乘矩阵,相当于对向量做线性变换,记变换后的结果为$Y$,则半正定矩阵可写成:$X^{T}Y \ge 0$,即为两个向量的内积,根据向量夹角公式有
所以半正定矩阵的含义:向量$X$经过$M$矩阵变换后的结果与自身的夹角小于等于$90^{\circ}$,这样的矩阵称为半正定矩阵
半正定判断
特征值判断
- 半正定:所有特征值都大于等于0
- 正定:所以特征值都大于0
matlab求特征值
A = [1 2 3; 4 5 6; 7 8 9];
[V, D] = eig(A); // V是特征向量,D是对应的特征值
V =
-0.2320 -0.7858 0.4082
-0.5253 -0.0868 -0.8165
-0.8187 0.6123 0.4082
D =
16.1168 0 0
0 -1.1168 0
0 0 -0.0000有负的特征值,所以A不是半正定矩阵
行列式判断
如果矩阵$M$的行列式$|M|$的各阶顺序主子式都大于0,则矩阵$M$为正定矩阵
如果奇数阶为负,偶数阶为正,则矩阵$M$为负定矩阵
应用
多元函数$f(\boldsymbol{x})$在点$\boldsymbol{x}_k$取极值的必要条件是
在$\boldsymbol{x}_k$点泰勒展开
令$\Delta \boldsymbol{x} = \boldsymbol{x} - \boldsymbol{x}_k$,代入可得
要让$\boldsymbol{x}_k$为极小值点,就必须保证$\boldsymbol{x}_k$领域内的一切$\boldsymbol{x}$,恒有$f(\boldsymbol{x}_k) < f(\boldsymbol{x})$,也就是$\Delta \boldsymbol{x}^{\mathrm{T}} \boldsymbol{H}(\boldsymbol{x}_k) \Delta \boldsymbol{x} > 0$,所以$\boldsymbol{H}(\boldsymbol{x}_k)$必须为正定矩阵
类似的,若要保证$\boldsymbol{x}_k$为极大值点,$\boldsymbol{H}(\boldsymbol{x}_k)$必须为负定矩阵
总结
对于多元函数$f(\boldsymbol{x})$,如果$\boldsymbol{x}_k$是驻点,也就是$\nabla f(\boldsymbol{x}_k) = 0$,那么
- 若$\boldsymbol{H}(\boldsymbol{x}_k)$为正定矩阵,则$\boldsymbol{x}_k$为极小值
- 若$\boldsymbol{H}(\boldsymbol{x}_k)$为负定矩阵,则$\boldsymbol{x}_k$为极大值
例子
求$f(\boldsymbol{x}) = x_1^2+x_2^2-6x_1-4x_2+9$的极值
先求梯度向量
再求Hessian矩阵
令$\nabla f(\boldsymbol{x}) = 0$可得驻点为$\boldsymbol{x}_k = \begin{bmatrix}3 & 2 \end{bmatrix}^\mathrm{T}$,又因为$\boldsymbol{H}(\boldsymbol{x}_k)$为正定矩阵,所以$\boldsymbol{x}_k$是极小值点,对应极小值为$f(\boldsymbol{x}) = -4$
matlab验证
n = [-10:0.1:10;-10:0.1:10];
[x1, x2] = meshgrid(n(1,:), n(2,:));
f = x1.^2 + x2.^2 - 6*x1 - 4*x2 + 9;
minval = min(min(f));
[row, column] = find(f == minval);
mesh(x1, x2, f);
x1(row, column);
x2(row, column);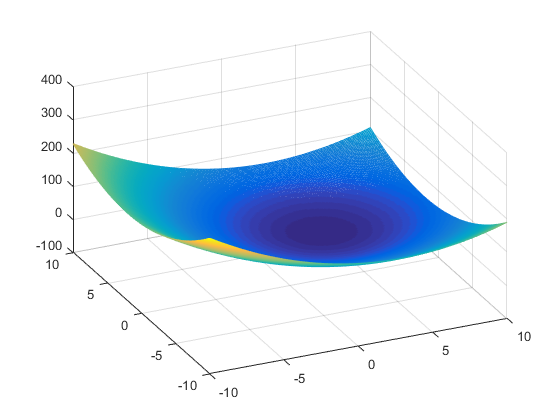
minval = -4
x1 = 3
x2 = 2

