多旋翼动力学

多旋翼动量定理

惯性系

$$m\dot{v} = mg + R \sum_{k=1}^{4}{F_k}$$

因为$F_k$是体轴系下多旋翼的升力，所以要左乘旋转矩阵转换到地理坐标系下
同时，因为$F_k$都是垂直于机体平面，沿体轴$z_b$方向，所以旋转矩阵只需要最后一列，展开写就是

$$m \begin{bmatrix} \ddot{x} \\ \ddot{y} \\ \ddot{z} \end{bmatrix} = m \begin{bmatrix} 0 \\ 0 \\ g \end{bmatrix} + (f_1+f_2+f_3+f_4) \begin{bmatrix} cos\psi sin\theta cos\phi + sin\psi sin\phi \\ sin\psi sin\theta cos\phi - sin\phi cos\psi \\ cos\theta cos\phi \end{bmatrix}$$

体轴系

$$m(\dot{v} + \hat{\omega}_b v) = R^\mathrm{T}mg + \sum_{k=1}^{4}{F_k}$$

$mg$是地理坐标系下的，左乘旋转矩阵的转置转换到体轴系

写成矩阵形式，体轴系下角速度为$\omega_b = \begin{bmatrix}p & q & r\end{bmatrix}^\mathrm{T}$

$$m \begin{bmatrix} \dot{u} \\ \dot{v} \\ \dot{w} \end{bmatrix} + m \begin{bmatrix} qw - rv \\ ru - pw \\ pv - qw \end{bmatrix} = mg \begin{bmatrix} -sin\theta \\ cos\theta sin\phi \\ cos\theta cos\phi \end{bmatrix} - \begin{bmatrix} 0 \\ 0 \\ f_1 + f_2 + f_3 + f_4 \end{bmatrix}$$

多旋翼动量矩定理

体轴系

$$I\dot{\omega} + \hat{\omega} I \omega = \sum_{k=1}^{4}{r_k \times F_k} - \hat{\omega} \sum_{k=1}^{4}{I_k\omega_k} - \sum_{k=1}^{4}{\tilde{\tau}_k}$$

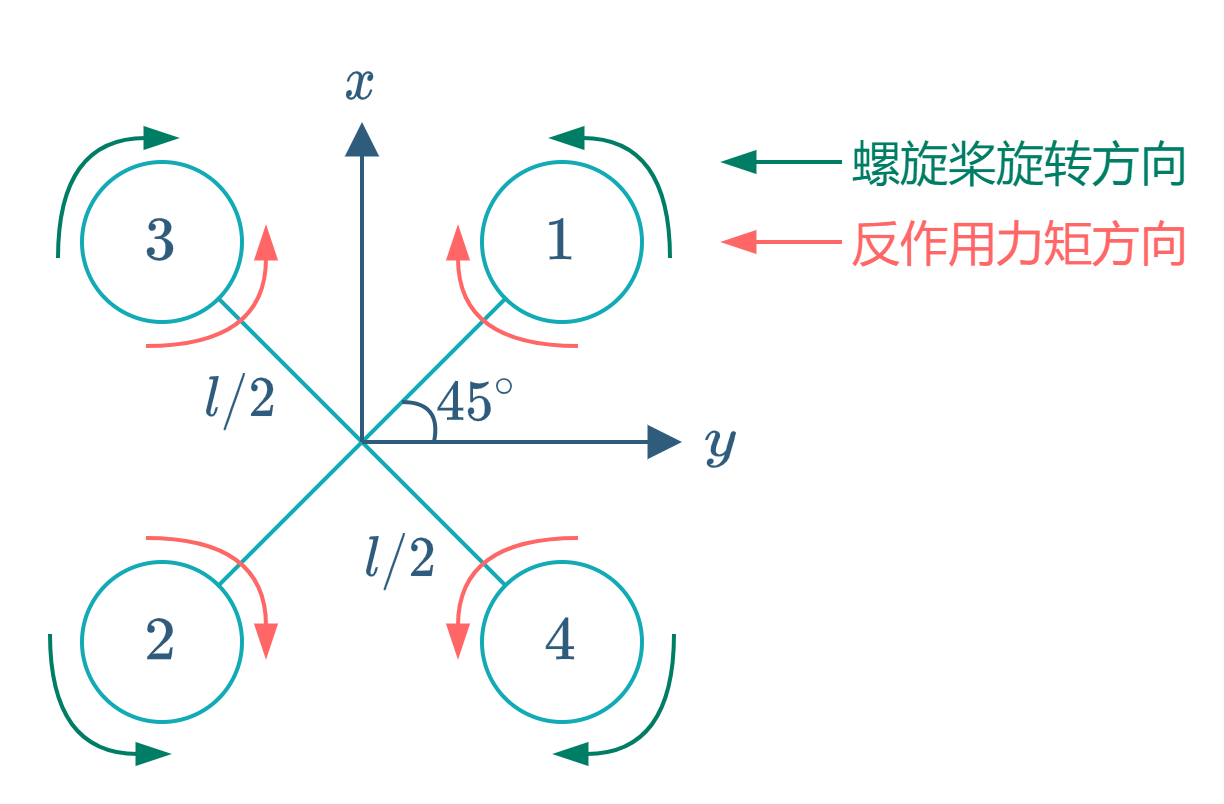
这里定义$z$轴垂直于机身向下
$\hat{\omega} \sum_{k=1}^{4}{I_k\omega_k}$称为陀螺力矩

$\omega_1 = \begin{bmatrix}0\\0\\ -\Omega_1 \end{bmatrix}\quad\omega_2 = \begin{bmatrix}0\\0\\ -\Omega_2 \end{bmatrix}\quad\omega_3 = \begin{bmatrix}0\\0\\ \Omega_3 \end{bmatrix}\quad\omega_4 = \begin{bmatrix}0\\0\\ \Omega_4 \end{bmatrix}$
$I_k$是螺旋桨的转动惯量，因为旋翼角速度垂直于自身，所以只需考虑旋翼$z$轴的转动惯量
所以

$$I_k = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & I_r \end{bmatrix}$$

所以

$$\sum_{k=1}^{4}{I_k\omega_k} = I_r \begin{bmatrix} 0 \\ 0 \\ -\Omega_1-\Omega_2+\Omega_3+\Omega_4 \end{bmatrix} \\ \hat{\omega} \sum_{k=1}^{4}{I_k\omega_k} = I_r \begin{bmatrix} 0 & -r & q \\ r & 0 & -p \\ -q & p & 0 \end{bmatrix} \begin{bmatrix} 0 \\ 0 \\ -\Omega_1-\Omega_2+\Omega_3+\Omega_4 \end{bmatrix} = \begin{bmatrix} I_r q (-\Omega_1-\Omega_2+\Omega_3+\Omega_4) \\ I_r p (\Omega_1+\Omega_2-\Omega_3-\Omega_4) \\ 0 \end{bmatrix}$$

$\tilde{\tau}_k$是电机给螺旋桨的扭矩
$\tilde{\tau}_1 = \begin{bmatrix}0\\0\\ -\tau_1 \end{bmatrix}\quad\tilde{\tau}_2 = \begin{bmatrix}0\\0\\ -\tau_2 \end{bmatrix}\quad\tilde{\tau}_3 = \begin{bmatrix}0\\0\\ \tau_3 \end{bmatrix}\quad\tilde{\tau}_4 = \begin{bmatrix}0\\0\\ \tau_4 \end{bmatrix}$

所以机体动量矩定理展开就是

$$\begin{align*} & I_x\dot{p} + (I_z-I_y)qr = \frac{\sqrt{2}}{4}l(-f_1+f_2+f_3-f_4) + I_rq(\Omega_1+\Omega_2-\Omega_3-\Omega_4) \\ & I_y\dot{q} + (I_x-I_z)pr = \frac{\sqrt{2}}{4}l(f_1-f_2+f_3-f_4) - I_rp(\Omega_1+\Omega_2-\Omega_3-\Omega_4) \\ & I_z\dot{r} + (I_y-I_x)pq = \tau_1 + \tau_2 - \tau_3 - \tau_4 \\ \end{align*}$$