无人机运动学

运动学与质量和受力无关，只研究位置，速度，姿态，角速度等参量

坐标系变换与旋转矩阵

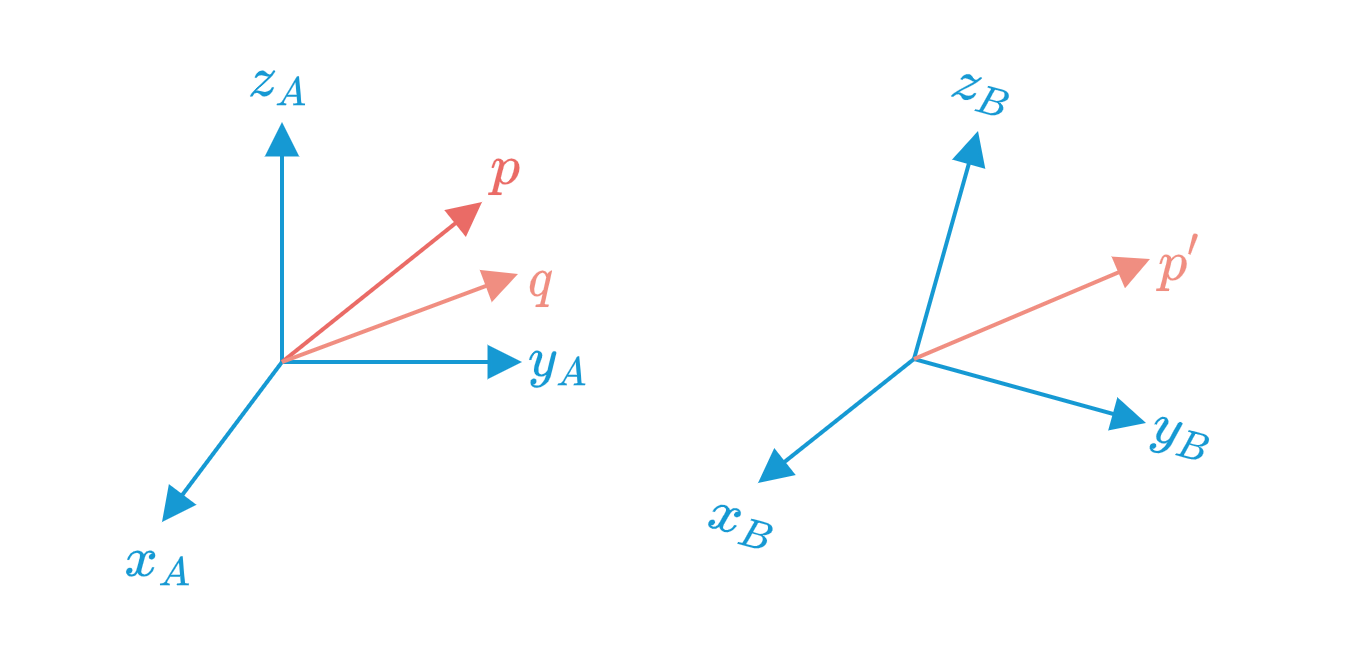
$p$在$\mathcal{A}$中的坐标为$\begin{bmatrix}p_1&p_2&p_3\end{bmatrix}^\mathrm{T}$，$p^{\prime}$在$\mathcal{B}$中的坐标也是$\begin{bmatrix}p_1&p_2&p_3\end{bmatrix}^\mathrm{T}$，旋转矩阵$R$的每一列是$\mathcal{B}$的三个基向量在$\mathcal{A}$中的投影。

$$\begin{bmatrix} \mathbf{x_B} & \mathbf{y_B} & \mathbf{z_B} \end{bmatrix} = \begin{bmatrix} \mathbf{x_A} & \mathbf{y_A} & \mathbf{z_A} \end{bmatrix} \cdot R$$

两边同乘以$\begin{bmatrix}p_1&p_2&p_3\end{bmatrix}^\mathrm{T}$，得到

$$\begin{bmatrix} \mathbf{x_B} & \mathbf{y_B} & \mathbf{z_B} \end{bmatrix} \begin{bmatrix}p_1\\p_2\\p_3\end{bmatrix} = \begin{bmatrix} \mathbf{x_A} & \mathbf{y_A} & \mathbf{z_A} \end{bmatrix} \cdot R \begin{bmatrix}p_1\\p_2\\p_3\end{bmatrix}$$

也就是$p^{\prime}$在$\mathcal{A}$中的坐标是$R\begin{bmatrix}p_1&p_2&p_3\end{bmatrix}^\mathrm{T}$
即把$p^{\prime}$移动到$\mathcal{A}$中，记为$q$，要得到$q$在$\mathcal{A}$中的坐标，需要左乘旋转矩阵$R$

$$\begin{bmatrix}q_1\\q_2\\q_3\end{bmatrix}=R\begin{bmatrix}p_1\\p_2\\p_3\end{bmatrix}$$

即

$$\mathbf{q}=R\mathbf{p}$$

这也可以看成在$\mathcal{A}$坐标系中，向量$p$通过旋转得到向量$q$。

例子

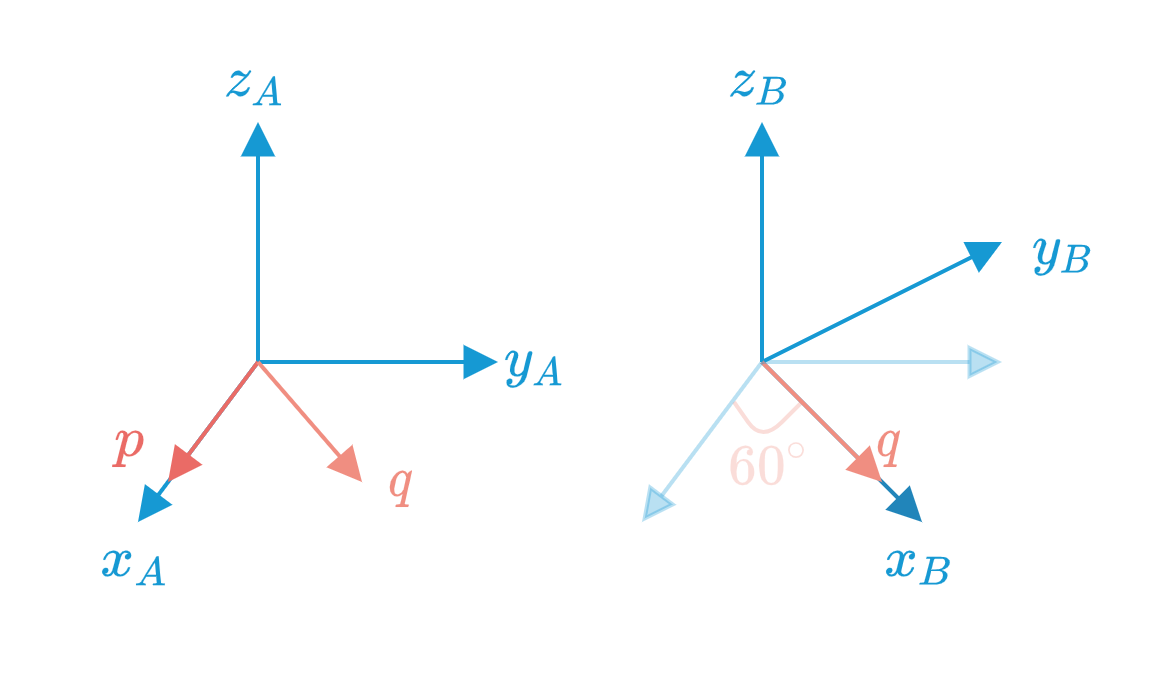
$\mathcal{A}$绕$z$轴旋转$60^{\circ}$得到$\mathcal{B}$，则$\mathcal{B}$中向量$\begin{bmatrix}1&0&0\end{bmatrix}^\mathrm{T}$在$\mathcal{A}$中的坐标为

$$\begin{bmatrix} \frac{1}{2} & -\frac{\sqrt{3}}{2} & 0 \\ \frac{\sqrt{3}}{2} & \frac{1}{2} & 0 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix}1\\0\\0\end{bmatrix} = \begin{bmatrix} \frac{1}{2} \\ \frac{\sqrt{3}}{2}\\ 0 \end{bmatrix}$$

也可以看成是$\mathcal{A}$中的向量$\mathbf{p}=\begin{bmatrix}1&0&0\end{bmatrix}^\mathrm{T}$绕$z$轴旋转$60^{\circ}$得到向量$\mathbf{q}=\begin{bmatrix}\frac{1}{2} &\frac{\sqrt{3}}{2}& 0\end{bmatrix}^\mathrm{T}$

旋转矩阵姿态运动学方程

对$\mathbf{q}=R\mathbf{p}$微分可得

$$\dot{\mathbf{q}}=\dot{R}\mathbf{p}$$

$\dot{\mathbf{q}}$是惯性系下的速度
两边同乘以$R^\mathrm{T}$，可得

$$R^\mathrm{T}\dot{\mathbf{q}}=R^\mathrm{T}\dot{R}\mathbf{p}$$

将方程转换到体轴系下，$R^\mathrm{T}\dot{\mathbf{q}}$是体轴系下的速度，根据

$$\dot{r}=\omega \times r$$

或者写成反对称阵形式

$$\dot{r}=\hat{\omega} \cdot r$$

$p$是体轴系下的向量，所以$R^\mathrm{T}\dot{R}$就是体轴系下的角速度的反对称形式，记为

$$\hat{\omega}_{b} = R^\mathrm{T}\dot{R}$$

也可以写成

$$\dot{R} = R\hat{\omega}_{b}$$

同理，由$\mathbf{q}=R\mathbf{p}$可得$\mathbf{p} = R^\mathrm{T}\mathbf{q}$，代入微分方程可得

$$\dot{\mathbf{q}}=\dot{R} R^\mathrm{T} \mathbf{p}$$

则$\dot{R} R^\mathrm{T}$就是惯性系下的角速度，记为

$$\hat{\omega}_{s} = \dot{R} R^\mathrm{T}$$

也可以写成

$$\dot{R} = \hat{\omega}_{s}R$$

参考Aerial Robotics

Rodrigues公式

任意旋转都可以用一个旋转轴$u$和一个旋转角$\phi$刻画

$$R(u, \phi) = Icos\phi + uu^\mathrm{T}(1-cos\phi) + \hat{u}sin\phi$$

$\hat{u}$是反对称阵(skew-symmetric matrix)，即$u=\begin{bmatrix}x&y&z\end{bmatrix}$

$$\hat{u}= \begin{bmatrix} 0 & -z & y \\ z & 0 & -x \\ -y & x & 0 \end{bmatrix}$$

即当已知旋转轴和旋转角度后，就可以通过Rodrigues公式求出旋转矩阵

欧拉角

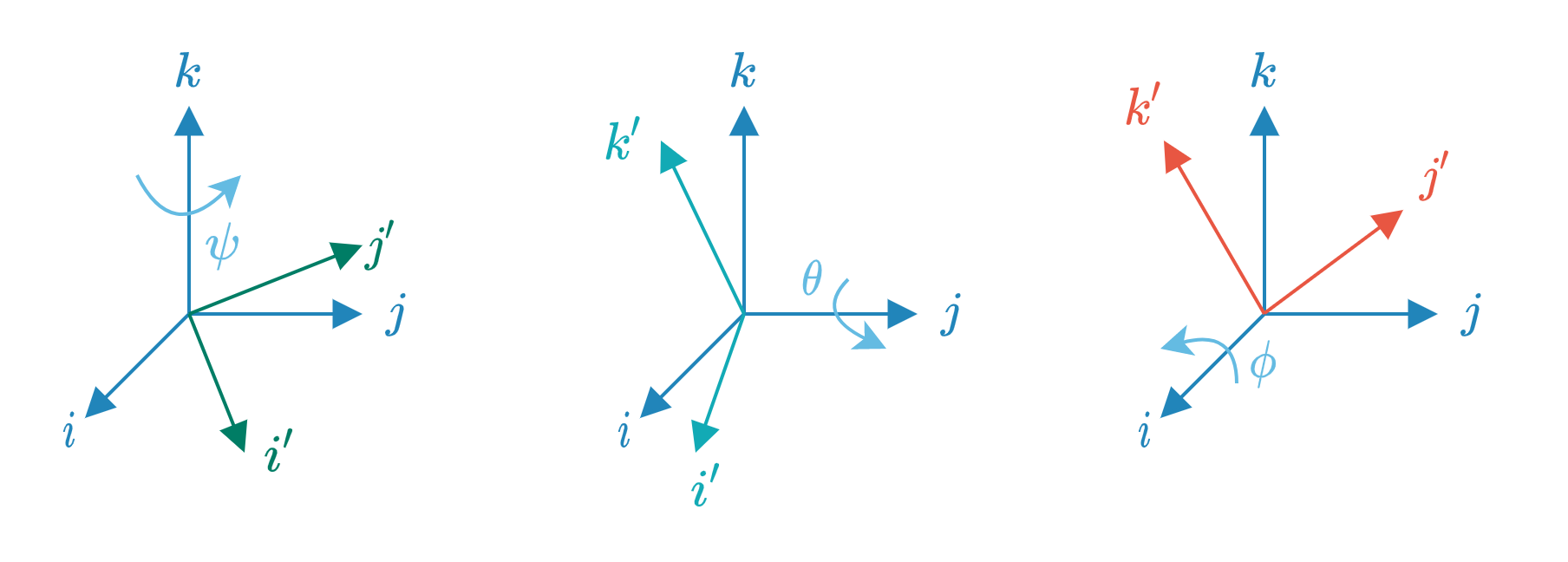
根据Rodrigues公式，可以写出绕$z$轴、$y$轴、$x$轴的旋转矩阵

绕$z$轴旋转$\psi$

$$R_Z(\psi) = \begin{bmatrix} cos\psi & -sin\psi & 0 \\ sin\psi & cos\psi & 0 \\ 0 & 0 & 1 \end{bmatrix}$$

绕$y$轴旋转$\theta$

$$R_Y(\theta) = \begin{bmatrix} cos\theta & 0 & sin\theta \\ 0 & 1 & 0 \\ -sin\theta & 0 & cos\theta \end{bmatrix}$$

绕$x$轴旋转$\phi$

$$R_X(\phi) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos\phi & -sin\phi \\ 0 & sin\phi & cos\phi \end{bmatrix}$$

按Z-Y-X的顺序组成三次旋转的复合旋转矩阵

$$R_Z(\psi)R_Y(\theta)R_X(\phi) = \begin{bmatrix} cos\psi cos\theta&cos\psi sin\theta \sin\phi-sin\psi cos\phi&cos\psi sin\theta cos\phi+sin\psi sin\phi\\ sin\psi cos\theta&sin\psi sin\theta sin\phi+cos\psi cos\phi&sin\psi sin\theta cos\phi-cos\psi sin\phi\\ -sin\theta&cos\theta sin\phi&cos\theta cos\phi \end{bmatrix}$$

这里每个旋转矩阵都是在新的坐标系中描述的，所以是右乘
如果是相对于原始坐标系，就要左乘。所以也可以看成是相对于原始坐标系的描述的X-Y-Z旋转复合

欧拉角姿态运动方程

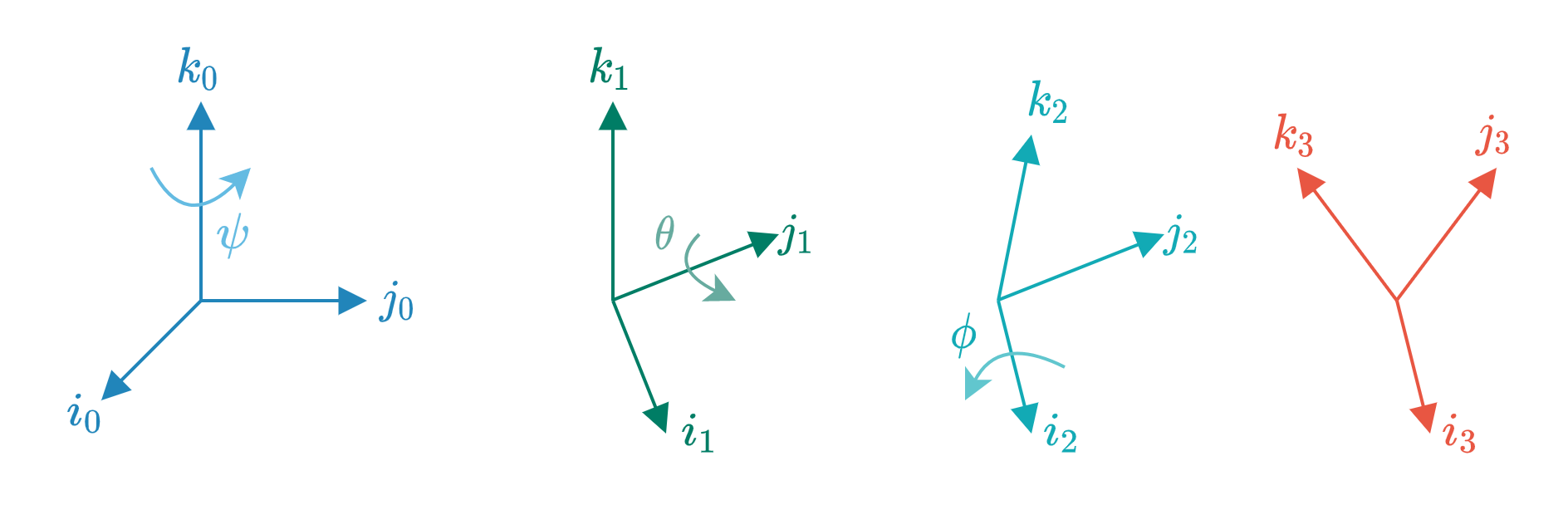
机体角速度可以表示为

$$\mathbf{\omega}= \begin{bmatrix}\mathbf{i}_3 & \mathbf{j}_3 & \mathbf{k}_3\end{bmatrix} \begin{bmatrix}p \\ q \\ r\end{bmatrix}$$

可以分解为三次变换的欧拉角速度组合

$$\mathbf{\omega} = \dot{\psi}\mathbf{k}_1 + \dot{\theta}\mathbf{j}_2 + \dot{\phi}\mathbf{i}_3$$

因为

$$\begin{bmatrix}\mathbf{i}_3 & \mathbf{j}_3 & \mathbf{k}_3\end{bmatrix} = \begin{bmatrix}\mathbf{i}_2 & \mathbf{j}_2 & \mathbf{k}_2\end{bmatrix} R_{32}$$

所以

$$\begin{bmatrix}\mathbf{i}_2 & \mathbf{j}_2 & \mathbf{k}_2\end{bmatrix} = \begin{bmatrix}\mathbf{i}_3 & \mathbf{j}_3 & \mathbf{k}_3\end{bmatrix} R_{32}^\mathrm{T}$$

所以

$$\mathbf{j}_2 = \begin{bmatrix}\mathbf{i}_3 & \mathbf{j}_3 & \mathbf{k}_3\end{bmatrix} \begin{bmatrix}0 \\ cos\phi \\ -sin\phi \end{bmatrix}$$

同理

$$\begin{bmatrix}\mathbf{i}_3 & \mathbf{j}_3 & \mathbf{k}_3\end{bmatrix} = \begin{bmatrix}\mathbf{i}_1 & \mathbf{j}_1 & \mathbf{k}_1\end{bmatrix} R_{21}R_{32}$$

所以

$$\begin{bmatrix}\mathbf{i}_1 & \mathbf{j}_1 & \mathbf{k}_1\end{bmatrix} = \begin{bmatrix}\mathbf{i}_3 & \mathbf{j}_3 & \mathbf{k}_3\end{bmatrix} R_{32}^{\mathrm{T}} R_{21}^{\mathrm{T}}$$

所以

$$\mathbf{k}_1 = \begin{bmatrix}\mathbf{i}_3 & \mathbf{j}_3 & \mathbf{k}_3\end{bmatrix} \begin{bmatrix}-sin\theta \\ sin\phi cos\theta \\ cos\phi cos\theta \end{bmatrix}$$

组合起来就是

$$\dot{\psi}\begin{bmatrix}-sin\theta \\ sin\phi cos\theta \\ cos\phi cos\theta \end{bmatrix} + \dot{\theta}\begin{bmatrix}0 \\ cos\phi \\ -sin\phi \end{bmatrix} + \dot{\phi}\begin{bmatrix}1 \\ 0 \\ 0 \end{bmatrix} = \begin{bmatrix} 1 & 0 & -sin\theta \\ 0 & cos\phi & sin\phi cos\theta \\ 0 & -sin\phi & cos\phi cos\theta \end{bmatrix} \begin{bmatrix}\dot{\phi} \\ \dot{\theta} \\ \dot{\psi}\end{bmatrix}$$

所以

$$\begin{bmatrix}p \\ q \\ r\end{bmatrix} = \begin{bmatrix} 1 & 0 & -sin\theta \\ 0 & cos\phi & sin\phi cos\theta \\ 0 & -sin\phi & cos\phi cos\theta \end{bmatrix} \begin{bmatrix}\dot{\phi} \\ \dot{\theta} \\ \dot{\psi}\end{bmatrix}$$

也可以写成

$$\begin{bmatrix}\dot{\phi} \\ \dot{\theta} \\ \dot{\psi}\end{bmatrix} = \begin{bmatrix} 1 & sin\phi tan\theta & cos\phi tan\theta \\ 0 & cos\phi & -sin\phi \\ 0 & sin\phi/cos\theta & cos\phi/cos\theta \end{bmatrix} \begin{bmatrix}p \\ q \\ r\end{bmatrix}$$

四元数

$$q = (q_0, q_1, q_2, q_3)$$

或写成

$$q = (q_0, \mathbf{q})$$

加减法

$$p \pm q = (q_0 \pm q_0, \mathbf{p} \pm \mathbf{q})$$

乘法

$$p \otimes q = (p_0q_0-\mathbf{p}^\mathrm{T}\mathbf{q}, p_0\mathbf{q}+q_0\mathbf{p}+\mathbf{p} \times \mathbf{q})$$

共轭

$$q^{*} = (q_0, -\mathbf{q})$$

逆

$$q^{-1} = \frac{q^{*}}{||q||}$$

已知旋转轴$u=\begin{bmatrix}u_1&u_2&u_3\end{bmatrix}^\mathrm{T}$和旋转角度$\phi$，可以写出四元数

$$q = (cos(\frac{\phi}{2}), u_1sin(\frac{\phi}{2}), u_2sin(\frac{\phi}{2}), u_3sin(\frac{\phi}{2}))$$

要对一个向量$p$进行旋转，先将向量写成四元数形式$p=(0, \mathbf{p})$，再左乘四元数$q$，右乘四元数的共轭$q^{-1}$

$$p^{\prime} = qpq^{*} = (0, \mathbf{p^{\prime}})$$

如果$q_1$是坐标系$\mathcal{A}$的四元数，$q_2$也是坐标系$\mathcal{A}$的四元数，则两次四元数的复合旋转是

$$q = q_2q_1$$

如果$q_1$是坐标系$\mathcal{A}$的四元数，旋转之后得到坐标系$\mathcal{B}$，$q_2$是坐标系$\mathcal{B}$的四元数，则两次旋转的复合是

$$q = q_1q_2$$

四元数姿态运动方程

$$\dot{q} = \frac{\mathbf{\omega}}{2} q$$

写成矩阵形式

$$\begin{bmatrix} \dot{q_0} \\ \dot{q_1} \\ \dot{q_2} \\ \dot{q_3} \\ \end{bmatrix} = \frac{1}{2} \begin{bmatrix} 0 & -\omega_x & -\omega_y & -\omega_z \\ \omega_x & 0 & \omega_z & -\omega_y \\ \omega_y & -\omega_z & 0 & \omega_x \\ \omega_z & \omega_y & -\omega_x & 0 \end{bmatrix} \begin{bmatrix} q_0 \\ q_1 \\ q_2 \\ q_3 \\ \end{bmatrix}$$

一阶龙格库塔求解

$$\begin{bmatrix} q_0 \\ q_1 \\ q_2 \\ q_3 \\ \end{bmatrix}_{t+\Delta t} = \begin{bmatrix} q_0 \\ q_1 \\ q_2 \\ q_3 \\ \end{bmatrix}_t + \frac{\Delta t}{2} \begin{bmatrix} 0 & -\omega_x & -\omega_y & -\omega_z \\ \omega_x & 0 & \omega_z & -\omega_y \\ \omega_y & -\omega_z & 0 & \omega_x \\ \omega_z & \omega_y & -\omega_x & 0 \end{bmatrix} \begin{bmatrix} q_0 \\ q_1 \\ q_2 \\ q_3 \\ \end{bmatrix}_t$$

代码实现

q0 = q0 + (-q1*wx - q2*wy - q3*wz)*halfT;
q1 = q1 + (q0*wx + q2*wz - q3*wy)*halfT;
q2 = q2 + (q0*wy - q1*wz + q3*wx)*halfT;
q3 = q3 + (q0*wz + q1*wy - q2*wx)*halfT;

四元数转欧拉角

$$\begin{bmatrix} \phi \\ \theta \\ \psi \end{bmatrix} = \begin{bmatrix} arctan(\frac{2(q_0q_1+q_2q_3)}{1-2(q_1^2+q_2^2)}) \\ arcsin(2(q_0q_2-q_1q_3)) \\ arctan(\frac{2(q_0q_3+q_1q_2)}{1-2(q_2^2+q_3^2)}) \end{bmatrix}$$

四元数表示旋转矩阵

坐标系$\mathcal{A}$到坐标系$\mathcal{B}$的旋转用四元数描述是$q$
则旋转矩阵可以表示为

$$R^A_B = \begin{bmatrix} q_0^2+q_1^2-q_2^2-q_3^2 & 2(q_1q_2-q_0q_3) & 2(q_1q_3+q_0q_2) \\ 2(q_1q_2 + q_0q_3) & q_0^2-q_1^2+q_2^2-q_3^2 & 2(q_2q_3-q_0q_1) \\ 2(q_1q_3-q_0q_2) & 2(q_2q_3+q_0q_1) & q_0^2-q_1^2-q_2^2+q_3^2 \end{bmatrix}$$

例子

坐标变换

旋转轴$u=\begin{bmatrix}0&0&1\end{bmatrix}^\mathrm{T}$，旋转角度$60^{\circ}$

$$\mathbf{q} = \begin{bmatrix}\frac{\sqrt{3}}{2} \\ 0 \\ 0 \\ \frac{1}{2}\end{bmatrix}$$

$q$在坐标系$\mathcal{A}$中的表示为

$$\begin{bmatrix} \frac{\sqrt{3}}{2} \\ 0 \\ 0 \\ \frac{1}{2} \end{bmatrix} \otimes \begin{bmatrix} 0 \\ 1 \\ 0 \\ 0\end{bmatrix} \otimes \begin{bmatrix} \frac{\sqrt{3}}{2} \\ 0 \\ 0 \\ -\frac{1}{2} \end{bmatrix} = \begin{bmatrix} 0 \\ \frac{1}{2} \\ \frac{\sqrt{3}}{2} \\ 0 \end{bmatrix}$$

所以在坐标系$\mathcal{A}$中向量$\mathbf{q}=\begin{bmatrix}\frac{1}{2} &\frac{\sqrt{3}}{2}& 0\end{bmatrix}^\mathrm{T}$

旋转复合

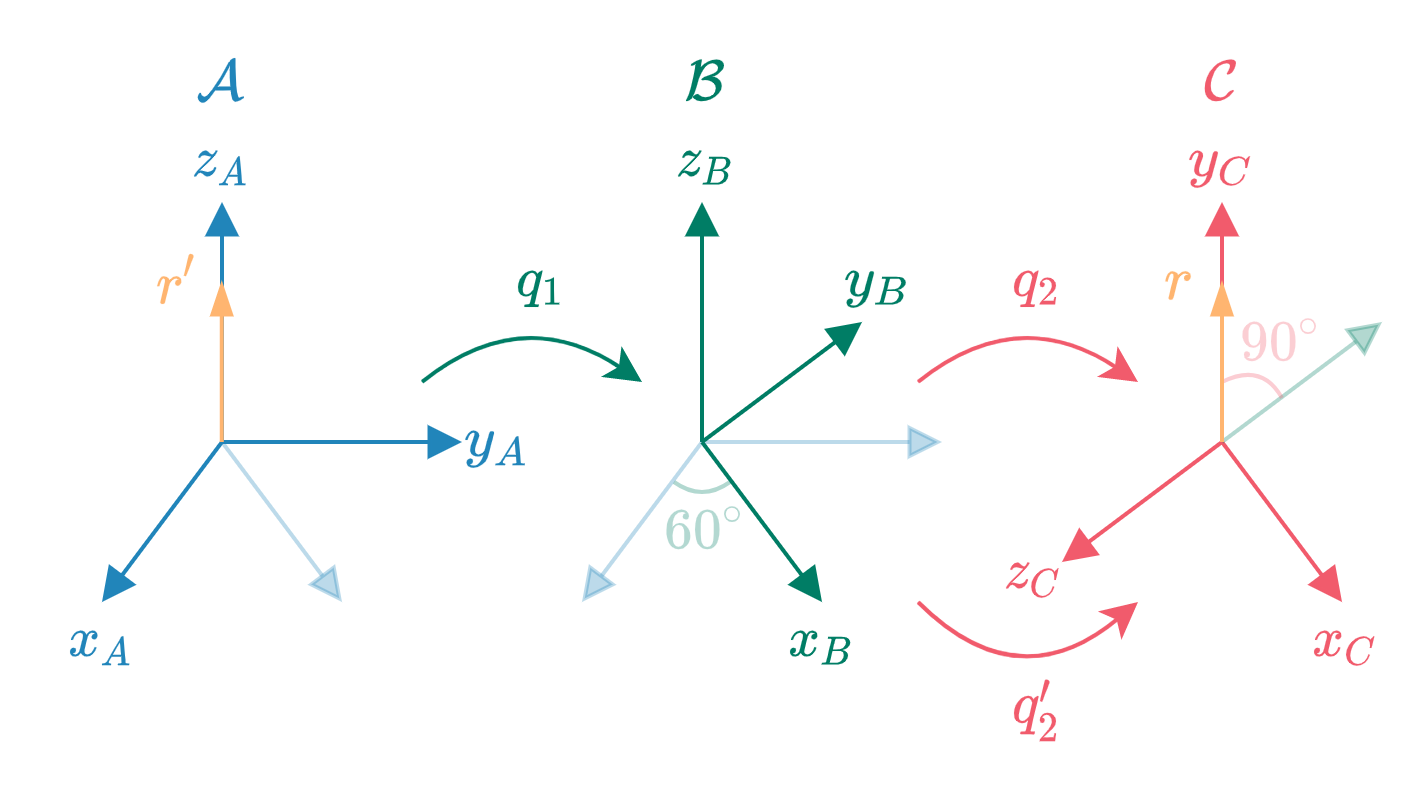
坐标系$\mathcal{A}$通过$q_1$旋转到坐标系$\mathcal{B}$，再通过$q_2$旋转到坐标系$\mathcal{C}$，其中$q_2$是在坐标系$\mathcal{B}$中的描述，$q_2^{\prime}$是在$\mathcal{A}$中的描述

$$q_1 = \begin{bmatrix}\frac{\sqrt{3}}{2} & 0 & 0 & \frac{1}{2}\end{bmatrix} ^\mathrm{T}$$ $$q_2 = \begin{bmatrix}\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} & 0 & 0\end{bmatrix} ^\mathrm{T}$$

$q_2^{\prime}$的旋转轴是$\begin{bmatrix}\frac{1}{2} &\frac{\sqrt{3}}{2}& 0\end{bmatrix}^\mathrm{T}$

$$q_2^{\prime} = \begin{bmatrix}\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{4} & \frac{\sqrt{6}}{4} & 0\end{bmatrix}^\mathrm{T}$$

两种表达的复合结果应该是一样的，只是乘的顺序不一样

$$q = q_1 \otimes q_2 = \begin{bmatrix}\frac{\sqrt{3}}{2} \\ 0 \\ 0 \\ \frac{1}{2}\end{bmatrix} \otimes \begin{bmatrix}\frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} \\ 0 \\ 0\end{bmatrix} = \begin{bmatrix}\frac{\sqrt{6}}{4} \\ \frac{\sqrt{6}}{4} \\ \frac{\sqrt{2}}{4} \\ \frac{\sqrt{2}}{4} \end{bmatrix}$$ $$q = q_2^{\prime} \otimes q_1 = \begin{bmatrix}\frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{4} \\ \frac{\sqrt{6}}{4} \\ 0\end{bmatrix} \otimes \begin{bmatrix}\frac{\sqrt{3}}{2} \\ 0 \\ 0 \\ \frac{1}{2}\end{bmatrix} = \begin{bmatrix}\frac{\sqrt{6}}{4} \\ \frac{\sqrt{6}}{4} \\ \frac{\sqrt{2}}{4} \\ \frac{\sqrt{2}}{4} \end{bmatrix}$$

坐标系$\mathcal{C}$中的向量$r=\begin{bmatrix}0 & 1 & 0 \end{bmatrix}^\mathrm{T}$在$\mathcal{A}$中的表示为

$$r^{\prime} = \begin{bmatrix}\frac{\sqrt{6}}{4} \\ \frac{\sqrt{6}}{4} \\ \frac{\sqrt{2}}{4} \\ \frac{\sqrt{2}}{4} \end{bmatrix} \otimes \begin{bmatrix}0 \\ 0 \\ 1 \\ 0 \end{bmatrix} \otimes \begin{bmatrix}\frac{\sqrt{6}}{4} \\ -\frac{\sqrt{6}}{4} \\ -\frac{\sqrt{2}}{4} \\ -\frac{\sqrt{2}}{4} \end{bmatrix} = \begin{bmatrix}0 \\ 0 \\ 0 \\ 1 \end{bmatrix}$$

由图可知是正确的

tips：四元数乘法的matlab编程实现

function result = quaternionMultiplication(q1,q2)
    result(1) = q1(1)*q2(1) - q1(2)*q2(2) - q1(3)*q2(3) - q1(4)*q2(4);
    result(2) = q1(1)*q2(2) + q1(2)*q2(1) + q1(3)*q2(4) - q1(4)*q2(3);
    result(3) = q1(1)*q2(3) - q1(2)*q2(4) + q1(3)*q2(1) + q1(4)*q2(2);
    result(4) = q1(1)*q2(4) + q1(2)*q2(3) - q1(3)*q2(2) + q1(4)*q2(1);
end